Video: Ո՞րն է Էյլերի բանաձևը՝ օգտագործելով քառաեդրոնի երեսների թիվը, որոնք ունեն գագաթներ որպես 4 և 6 եզրեր:
2024 Հեղինակ: Stanley Ellington | [email protected]. Վերջին փոփոխված: 2023-12-16 00:18
Այս էջը թվարկում է ապացույցները Էյլերի բանաձեւ : համար ցանկացած ուռուցիկ բազմանիստ, ի թիվ -ից գագաթները և դեմքեր միասին ուղիղ երկուսով ավելի է, քան թիվ -ից եզրեր . Խորհրդանշականորեն V−E+F=2. Համար օրինակ, ա քառաեդրոն ունի չորս գագաթներ , չորս դեմքեր , և վեց եզրեր ; 4 - 6 + 4 =2.
Հետևաբար, որքա՞ն կլինի երեսների թիվը, եթե կա 6 գագաթ և 12 եզր։
Խորանարդը կամ խորանարդը եռաչափ ձև է, որն ունի 12 եզր , 8 անկյունները կամ գագաթները , և 6 դեմք.
Կարելի է նաև հարցնել՝ ինչպե՞ս է գործում Էյլերի բանաձևը։ Էյլերի բանաձեւը , Լեոնհարդի երկու կարևոր մաթեմատիկական թեորեմներից որևէ մեկը Էյլեր . Առաջինը տոպոլոգիական անփոփոխություն է (տես տոպոլոգիա), որը կապում է ցանկացած պոլիէդրոնի դեմքերի, գագաթների և եզրերի քանակը։ Գրված է F + V = E + 2, որտեղ F-ը երեսների թիվն է, V-ը՝ գագաթների, իսկ E-ը՝ եզրերի թիվը։
Ո՞րն է խորանարդի դեմքերի գագաթների և եզրերի քանակի հարաբերությունների բանաձևը:
V - E + F = 2; կամ, բառերով ասած թիվ -ից գագաթները , հանած թիվ -ից եզրեր , գումարած դեմքերի քանակը , հավասար է դեպի երկու.
Ո՞րն է Էյլերի պոլիէդրոնի բանաձևը:
Այս թեորեմը ներառում է Էյլերի բազմանիստ բանաձևը (երբեմն կոչվում է Էյլերի բանաձեւը ) Այսօր մենք այս արդյունքը կասենք հետևյալ կերպ. V գագաթների, F երեսների և E եզրերի թիվը ուռուցիկ եռաչափում: բազմանիստ , բավարարում է V + F - E = 2:
Խորհուրդ ենք տալիս:
Արդյո՞ք այն գործընթացը, որը փոխակերպում է մուտքերը ելքերի, որոնք կարող են վաճառվել որպես ապրանքներ և ծառայություններ:
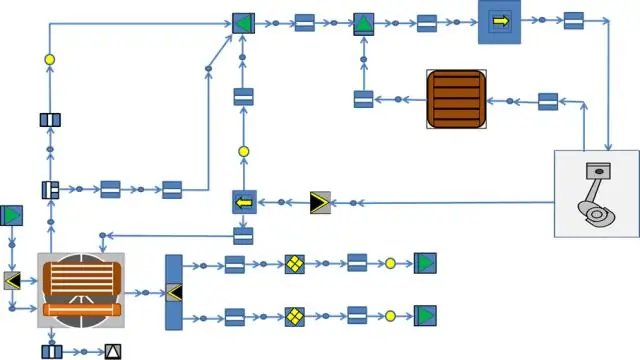
Գործառնությունների կառավարումը մուտքերը (աշխատուժ, կապիտալ, սարքավորումներ, հող, շենքեր, նյութեր և տեղեկատվություն) փոխակերպում է արտադրանքի (ապրանքների և ծառայությունների), որոնք ապահովում են հաճախորդներին հավելյալ արժեք: Բոլոր կազմակերպությունները պետք է ձգտեն առավելագույնի հասցնել իրենց փոխակերպման գործընթացների որակը՝ հաճախորդների կարիքները բավարարելու համար
Որքա՞ն է արտադրության ընդհանուր ծախսերը `օգտագործելով ճկուն բյուջե:
Ըստ արտադրության ճկուն բյուջեի, արտադրության ակնկալվող ընդհանուր արժեքը ստանդարտ ծավալով (20,000 մեքենա-ժամ) կազմում է 100,000 ԱՄՆ դոլար, ուստի ստանդարտ վերգետնյա փոխարժեքը 5 դոլար է մեկ մեքենայ/ժամի համար (100,000 ԱՄՆ դոլար/20,000 մեքենա-ժամ)
Ինչպե՞ս եք գտնում միավորի արտադրանքի արժեքը՝ օգտագործելով ավանդական ինքնարժեքը:
Գումարեք ձեր ընդհանուր ուղղակի նյութերի ծախսերը, ձեր ընդհանուր ուղղակի աշխատուժի ծախսերը և ձեր ընդհանուր արտադրության ընդհանուր ծախսերը, որոնք դուք կրել եք այդ ժամանակահատվածում, որպեսզի որոշեք ձեր արտադրանքի ընդհանուր ծախսերը: Բաժանեք ձեր արդյունքը տվյալ ժամանակահատվածում ձեր արտադրած ապրանքների քանակով, որպեսզի որոշեք ձեր արտադրանքի արժեքը մեկ միավորի համար
Ինչպե՞ս եք հաշվարկում ՀՆԱ-ն՝ օգտագործելով ավելացված արժեքի մոտեցումը:
Այն չափում է տնտեսության մեջ արտադրված բոլոր ապրանքների և ծառայությունների ընդհանուր արժեքը որոշակի ժամանակահատվածում: Այն կարող է հաշվարկվել երեք տարբեր եղանակներով՝ ավելացված արժեքի մոտեցում (ՀՆԱ = VOGS – IC), եկամտի մոտեցում (ՀՆԱ = W + R + i + P + IBT + D) և ծախսերի մոտեցում (ՀՆԱ = C +): I + G + NX)
Որոնք են այն նյութերը, որոնք օգտագործվում են որմնադրությանը:
Քարտաշինության ընդհանուր նյութերն են աղյուսը, շինարարական քարը, ինչպիսիք են մարմարը, գրանիտը և կրաքարը, ձուլածո քարը, բետոնե բլոկը, ապակե բլոկը և թրթուրը: